A9 - Morphological Operation

Today, we'll all talk about shapes... shapes... shapes...

When I hear the word morphology, the first thing that comes to my mind is the biological context related to the study of structures and forms of plants and animals. Basically, this instinctive definition of mine can be stretched out to the image processing context. Practically, it means the same thing but instead of organisms, we talk about anything with no life like shapes.

Moving one step forward, morphological operations are then operations on an image that transform it to another for further processing and information extraction. These operations apply a structuring element (sort of a basis image) to an input image, creating an output image of the same size as the structuring element.

The most common type of morphological operations are dilation and erosion.

A8 - Enhancement in the Frequency Domain

Today is July 21, 2011 -- exactly 5 weeks after I put up this blog... It was fun writing notes and nerdy stuff here knowing the fact that anybody, anywhere around the globe, can actually reach and read this blog. Amazing huh!

Anyway, going back to what this post really is about, I will show you how to enhance an image by removing or improving some parts in the frequency domain. To be able to follow the concepts I will use in this post, you must have some background in using Fourier Transform, if not, you can visit first my previous posts here and here.

The basic idea of this post is that whenever we have an image with repetitive patterns which are not necessary, we can get its Fourier Transform. By doing so, we are now in the frequency domain so we can create a filter that will remove frequencies pertaining to the unwanted patterns. And viola! The unwanted patterns are gone!

A7 - Properties of the 2D Fourier Transform

This time around, I would be talking about something you guys are familiar with already, FOURIER TRANSFORM. But just in case it's the first time you visit my blog, I suggest you read through first 2 days old post about Fourier Transform here.


With the use of my good friend Scilab, I'll show you what happen to different patterns when operated by Fourier Transform (FT). Recall that we can directly get the Fourier Transform in Scilab by using the function fft2() and shifting its quadrants using fftshift(). (Remember to take the absolute value first using abs() before shifting.)

The patterns I used here are 128x128 images of square, annulus, square annulus, two symmetric slits along the x-axis and two symmetric dots along the x-axis. Results are shown below

Figure 1. (A) square (B) annulus (C) square annulus (D) two symmetric slits

(E) two symmetric dots (F-J) Corresponding FT of A to E

Just in case you wonder what the FT really looks like because the pattern produced is not really obvious, we can play a trick by creating smaller versions of A to E (not image size wise) and take their FT's.

Figure 2. (A) square (B) annulus (C) square annulus (D) two symmetric slits

(E) two symmetric dots (F-J) Corresponding FT of A to E

Now that looks clearer now. Figure 1 and 2 provides us a small bank of the Fourier Transform of some common basic patterns observable in real life optical systems. These correspondences are often called Fourier Transform (FT) pairs. Oftenly, it is helpful and saves time to know the FT pair of common patterns beforehand instead of deriving each everytime you need it.

We now proceed to the anamorphic property of Fourier Transform. Anarmophic according  to [2] is the production of an optical effect along mutually perpendicular radii. Basically, we'll talk about the FT of sinusoids and the corresponding modifications to it when we try distorting the sinusoids. 

As a start, let's observe the FT of a simple sinusoid with varying frequency of the form z = sin(2*pi*f*x). 

 

Figure 3. (A-F) Sinusoids of frequency 2, 4, 6, 8, 10 and 20 Hz.

(G-L) Complementary FT of A to F.

We can see that the FT of a sinusoid produces two identical peaks symmetric about the center of the image and along the axis of the sinusoid. This is indeed true since FT decomposes a signal to its consequent frequencies. Thus, the two peaks represent two frequencies for a sinusoid which are equal and just negation of each other. On the other hand, we can observe that as the frequency of the sinusoid increases, the peaks move upward/downward. This is because the derived component frequencies go higher and moves further away from the center.

If we try adding a constant bias to a sinusoid or technically shifting its value to the positive region, the outcome is

 

Figure 4. (A) Sinusoid of frequency 4Hz with 

added constant bias of 1. (B) FT of A.

In figure 4B, we notice another peak present in the center of the image (try clicking the image to enlarge). The reason for the center peak is that another component was separated by FT with 0 Hz frequency corresponding to the added constant bias. This is factual because a sinusoid (sine) with 0 frequency is a constant. This observation can be useful in finding actual frequencies in interferograms with DC biases. Just remove the 0 frequency peak and the observed frequencies will then be correct.

Suppose however a non-constant bias(another sinusoid with low frequency) is added, what happens to the FT? 

Figure 5. (A) Sinusoid of frequency 4Hz with 

added 0.5Hz sinusoid bias. (B) FT of A.

Looking at figure 5, we can still apply the same reasoning of removing the peaks very close to 0 to get the actual frequencies of an interferogram.

We further move one step higher by rotating our sinusoid with respect to different angles. Just change the sinusoid to the form

theta_deg = 30;
theta = theta_deg*(%pi/180);
z = sin(2*%pi*f*(y*sin(theta) + x*cos(theta)));

Note: The conversion of theta_deg to theta is necessary because the argument supported by Scilab trigonometric functions is radians. 

 

Figure 6. (A-F) Sinusoids of frequency 4Hz rotated by 30, 60, 

90, 120, 150 and 180 degrees. (G-L) FT's of A to F.

We can observe that as the rotation angle increases, the peaks move counterclockwise about an angle equal to the rotation angle. The important artifact to remember is that the rotation did not change the presence of two frequencies as observed in figure 3H. The FT simply rotated as a result of the rotation of the sinusoid.

If we are then to create a sinusoid as a result of multiplication of two perpendicular sinusoids,

 z = sin(2*%pi*4*x).*sin(2*%pi*4*y);

the following result happens

 

Figure 7. (A) Sinusoid as a result to multiplication of 4Hz 

sinusoids along x and y. (B) FT of A.

The result shown in figure 7B suggests that the peak frequencies doubled instead of the usual two and they went off the center axes. The doubling phenomena happened because the two frequencies corresponding for each sinusoid along a certain position paired up. In particular, the observed peaks correspond to combinations of 4 and -4Hz along the x-direction with the 4 and -4Hz along the y-direction. The locations would then be at (4,4), (4,-4), (-4,4) and (-4,-4).

As curiosity-driven people, we can try combining the sinusoid described in figure 7A with one rotated sinusoid as shown

 

Figure 8. (A-G) Figure 7A with added single rotated 

sinusoid with angles 0, 30, 60, 90,120, 150, 180 

degrees respectively.

A good prediction would be that the FT will four frequencies as shown in figure 7B can still be seen with additional frequencies rotated. Basically, just integrate figure 7B with figures 6G-6L individually.

 

Figure 9. (A-G) FT of figures 8A-G, respectively.

Aha! We had a correct prediction! What if we try to incorporate 6 sinusoids rotated an angle 30, 60, 90, 120, 150, and 180 at the same time to figure 7A. I must say that the resulting FT should look like a superposition of figures 9B-G. And since the chosen angles somewhat form half of a full rotation, I think the FT would have a circle in the middle.

Figure 10. (A) Combination of 1 multiplication of two perpendicular

sinusoids and 6 rotated sinusoids. (B) FT of A.

Indeed, the formed pattern has a circle inside!! 

In conclusion, this activity was pretty much a good one for understanding Fourier Transform deeper. The key idea is that whenever we combine sinusoids and produce complicated patterns, the Fourier Transform decomposes the frequencies we used to provide a clearer picture on the operations we used to create the pattern.

For this activity, I would give myself a grade of 10.0 for producing all the outputs necessary and for giving clear figures that explains the objectives.

References:

[1] 'Properties of the 2D Fourier Transform', 2010 Applied Physics 186 manual by Dr. Maricor Soriano

[2] http://www.thefreedictionary.com/anamorphic

A6 - Fourier Transform Model of Image Formation

If you would ask a physicist some terms or concepts commonly used in his/her field, Fourier Transform may have a good chance coming out. You know, Fourier Transform may sound so creepy to guys doing something far from physics, but it's just a piece of mathematical tool that does great wonder =)

Fourier transform decomposes a signal into its component frequencies. It has a wide range of application, from optics to signal and image processing and to real life devices such as spectroscopy to magnetic resonance imaging [2].

In strict mathematical definition, the Fourier Transform(FT) of an two dimensional image f(x,y) is

Equation 1. Fourier transform

where fx and fy are the component frequencies along x and y. However, if you don't have a background in programming, you would ask how to implement equation 1 numerically. The answer would be to discretized equation 1 in the form

Equation 2. Discrete Fourier Transform

where xo and yo are spatial intervals between consecutive signal samples in the x and y [3]. In most programming software, the implementation is called a Fast Fourier Transform (FFT). In Scilab, the function is fft2().

The output of the FFT is a complex number array where the diagonals of its quadrant interchanged as shown below

Figure 1. Quadrant conversion from image to FFT output.

 To see what fft2 in Scilab can do, we apply it to a 128x128 image of a white circle and letter "A".

Figure 2. (A) binary image of a circle. (B) circle FFT. (C) circle shifted FFT. 

(D) circle inverse FFT. (E) binary image of "A". (F) "A" FFT. 

(G) "A" shifted FFT. (H) "A" inverse FFT.

Figures 2A and 2E are the images of a circle and letter "A" created using Scilab and Paint. We then use the fft2() of Scilab to get the Fourier transform of these images as shown in 2B and 2F. However, since the output of an FFT is a complex array, we must take its intensity value instead using abs(). 

Taking note of the quadrant shifting described in figure 1, the results of 2B and 2F must be shifted back to original quadrant orientation using  fftshift(). The results can be seen at figures 2C and 2G and it can be noted that 2C is actually verifying the analytical Fourier Transform of a circle. To check whether the obtained FFT results are correct, an inverse FFT is done by taking the FFT of the results of 2C and 2G. The corresponding results are shown in 2D and 2H which are obviously (well for letter "A") inverted. 

Now, after familiarizing ourselves with FFT, we now move one step higher by introducing my friend Mr. Convolution. Convolution practically is just a combination of two functions producing a modified version of the two. Mathematically speaking, it is expressed as 

 

Equation 3. Convolution integral

We now take use of this beautiful convolution integral by simulating an imaging device. Yes, an imaging device! Suppose you have a camera or something that has a lens in it, if you try covering parts of the lens, what effects do you observe in the image output? Hmmm... Verify your intuition by reading further.

So we create a 128x28 image of the letters "VIP" filling up approximately 50% of the space (figure 3) and a white circle same as in figure 2A. The letters will serve as our image to be captured and the circle as our aperture. 

 Figure 3. Created "VIP" image.

We can implement equation 3 by first taking the FFT fft2() of figure 3 and fftshift() of figure 2A. To get the convolved image, we get the inverse of the product of their FFT. If we do this for circles of different radii, the results will be as follow

 

Figure 4. (A-E) Circular apertures of radii 0.1, 0.3, 0.5, 0.7 and 0.9.

(F-J) Convolved images corresponding to apertures in A to E.

We may observe that the resulting images are inverted as compared to the original image figure 3. And as the aperture's radii decreases, the images' resolution decreases as well becoming "blurrier". This is practically true in real life as less light enters the device and thus producing low quality image.

After saying hi to Mr. Convolution, I want you to meet Mr. Correlation. From the word's English definition, correlation is indeed the measure of similarity between two objects or in our case two functions. If you're interested with its mathematical expression, it is 

Equation 4. Correlation function p.

At first glance, it pretty looks like the same as the convolution integral, but it's not. The only chance they become equal is that when f and g are even functions. cool!

But where do we use Mr. Correlation? --> We can use it for pattern recognition or template matching. I'll tell you how.

We first create a 128x128 image of a text "THE RAIN IN SPAIN STAYS MAINLY IN THE PLAIN." We will try to recreate this text using 128x128 image of the letter "A" with the same font and font size as with the text. We then take the inverse FFT of the product of the FFT of "A" and the conjugate of the FFT of the text. In Scilab, the easier way to take a conjugate is by using conj(). If you got a bit confused, a snippet of the code is output = fft2(Fa.*(conj(Ftext))) where Fa is the FFT of "A" and Ftext is the FFT of the text. Results are

  

Figure 5. (A) Text. (B) letter "A". (C) output. (D) shifted FFT of C.

It can be seen in figure 5D that the text is somewhat mimic to some extent. Locations of letter "A" produced the highest correlation translating to a brighter image which indeed brought the idea that correlation can be actually used in finding words in a document.

Another template matching application is edge detection where the edge pattern is matched with an image. We can implement this by making a 3x3 matrix of an edge pattern where a value of negative -1 can be treated as an edge. (NOTE: total sum must be zero!). In Scilab we can create different edge patterns such as horizontal, vertical, diagonal and spot by using the matrices

pattern_hor = [-1 -1 -1; 2 2 2; -1 -1 -1];

pattern_ver = [-1 2 -1; -1 2 -1; -1 2 -1];

pattern_diag = [-1 -1 2; -1 2 -1; 2 -1 -1];

pattern_spot = [-1 -1 -1; -1 8 -1; -1 -1 -1];

These pattern matrices are convolved with the VIP image as in figure 3 using the Scilab function imcorrcoef(grayscale image, pattern). Results are shown below.

Figure 6. (A) horizontal pattern. (B) vertical pattern. (C) diagonal pattern.

(D) spot pattern. (E-H) Convolved image of VIP with A-D.

We can see from the results of figure 6, the resulting convolved image follows the edges feed into them. Horizontal pattern makes the horizontal edges of VIP more pronounced while vertical pattern highlights the vertical edges. The spot pattern in turn created the clearest edge detection result due to the fact that it somewhat combines the horizontal and vertical patterns.

Woohoo! This was a fun activity, I learned a lot... I already have thoughts of applying the methods in my future works. 

I would probably give myself a grade of 10.0 for producing all the outputs needed in this activity and producing good figures to back my results.

References:
[1] 'Fourier Transform Model of Image Formation', 2010 Applied Physics 186 manual by Dr. Maricor Soriano
[2] http://en.wikipedia.org/wiki/Fourier_transform#Applications
[3] http://fourier.eng.hmc.edu/e101/lectures/Image_Processing/node6.html

A5 - Enhancement by Histogram Manipulation

Image is an imitation of the form of an object, place or a person. Appreciation towards images is often proportional to the extent of its quality. However, quality may be affected by many different factors such as lighting, camera resolution, type of focus method, to name a few.

So how do we improve the quality of an image without repeating image acquisition?

--->> The answer is through histogram manipulation.

An image histogram provides us a quick look on the tonal distribution of an image. We can then enhance the quality or certain features of an image by manipulating its pixel value. I'll show you how to do this in this blog post.

First, we obtain from our collection a picture/image that seems to be dark in its nature.

 

Figure 1. Image to be enhanced. 

(image taken from http://baisically.blogspot.com/2011/01/sad-panda-8.html)

We convert the image into grayscale mode and take its histogram. We then obtain the cumulative distribution function(CDF) from the probability distribution function(PDF) or the normalized histogram. In Scilab, this can be done by using the cumulative sum function cumsum(x) where x is a matrix or vector. In simple terms, CDF is the probability that a value will be found less than or equal to an x value.

 Figure 2. Enhancement preliminaries. (a) Grayscale conversion of figure 1.

(b) Grayscale histogram of figure 1. (c) CDF of normalized version of (b).

We do the enhancement by backprojecting the image pixel values to the pixel value of our desired CDF. For example, our desired CDF is a straight increasing line.

Figure 3. Backprojecting method.

We take a grayscale value of x1 and find its CDF value y1. We then trace y1 in the desired CDF as y2. After tracing y1 to y2, we get the corresponding grayscale value x2 of y2. Finally, we replace x1 by x2 in the image concerned. We repeat the process for all grayscale values from 0-255 of our original CDF.

Since we now know the backprojecting method, we create different desired normalized CDF's of linear and nonlinear form.

 

Figure 4. Different desired CDF's. (a) Linear. (b) Quadratic. (c) Cubic.

(d) Gaussian. (e) Logarithmic. (f) Hyperbolic tangent

The CDF's are acquired using the code snippet below:

grayscale = 0:255;

cdf_linear = (1/255)*grayscale;   //linear CDF
cdf_quadratic = ((1/255)*grayscale).^2;   //quadratic CDF
cdf_cubic = ((1/255)*grayscale).^3;    //cubic CDF

a_gauss = 0.01; b_gauss = -((1/255)^2)*log(100);
cdf_gaussian = a_gauss*exp(-b_gauss*grayscale.^2);   //gaussian CDF  Note: cdf value from 0.01 to 1.

a_ln = (exp(1)-1)/255; b_ln = 1;
cdf_ln = log(a_ln*grayscale + b_ln);    //logarithmic CDF 

b_tanh = atanh(-0.99); a_tanh = (1/255)*(atanh(0.99)-b_tanh);
cdf_tanh = (tanh(a_tanh*grayscale + b_tanh))/1.98 + 0.5;     //hyperbolic tangent CDF

To get the corresponding new grayscale values of 0:255 depending on the desired CDF, we invert the equations of our desired CDF's which in turn makes the CDF values of our original image (cdf_original) as our independent variable. You can follow the code snippet below.

grayscale_linear = round(255*cdf_original);
grayscale_quadratic = round(255*sqrt(cdf_original));
grayscale_cubic = round(nthroot((255^3)*cdf_original, 3));
grayscale_gaussian = round(sqrt(-log(cdf_original/a_gauss)/b_gauss));
grayscale_ln = round((exp(cdf_original)-b_ln)/a_ln);
grayscale_tanh = round(1/a_tanh*(atanh(1.98*(cdf_original-0.5))-b_tanh));

After applying the method as described above, the resulting modified images are

 

Figure 5. Modified images based from a CDF of (a) linear, (b) quadratic,

(c) cubic, (d) gaussian, (e) logarithmic and (f) hyperbolic tangent.

To be able to verify whether the modified images have the desired CDF, we take their corresponding normalized histograms(or pdf) and get their CDF.

Figure 6. Histograms based on the CDF type of (a) linear, (b) quadratic,

 (c) cubic, (d) gaussian, (e) logarithmic and (f) hyperbolic tangent.

Figure 7. Retrieved CDF of modified images based on the CDF type of 

(a) linear, (b) quadratic, (c) cubic, (d) gaussian, (e) logarithmic and (f) hyperbolic tangent.

Looking at figures 4 and figures 7, we can say that the CDF's are exactly the same suggesting that the backprojecting method is indeed effective.

Now, we comment on the alteration of the original image according to a particular CDF.

• For a linear CDF, the image became brighter and seems to be equalized.
• For a quadratic CDF, the image is brighter as compared to using a linear CDF.
• For a cubic CDF, the image is even brighter as compared to both the linear and quadratic CDF.
• For a pseudo-gaussian CDF, the image became very bright insinuating image overexposure.
• For a logarithmic CDF, the image is similar to when using a linear CDF with only slight increment in the presence of almost black colors.
• For a hyperbolic tangent CDF, the image became grayish since the histogram shows that more values can be found in the gray region.

The procedure above is coded personally using a programming language, however there are available freewares online that do histogram manipulation. One of the common freeware is GNU Image Manipulation Program (GIMP). A copy of which can be found here. GIMP is a very powerful image processing software comparable to Adobe photoshop.

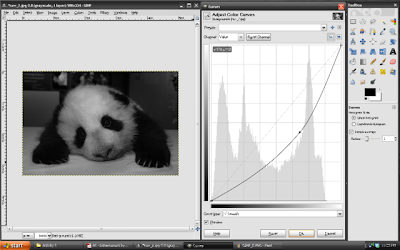
In GIMP, histogram manipulation can be made by first opening your desired image. You can then convert this into grayscale by clicking the Image button and choosing Grayscale in the Mode selection. To automatically graph the histogram of the grayscaled version of your image, click Colors and choose Curves. To start histogram manipulation, just drag the diagonal straight line in the Curves window and observe the changes in the image at the main window. Snapshots of different diagonal line orientations are shown below.

Figure 8. Sample histogram manipulation in GIMP.

 Figure 9. Another sample histogram manipulation using GIMP.

That's it! You can choose whatever CDF you want depending on what effect you would want to happen on your image. Enjoy image enhancement  in the future!

As a conclusion, I would give myself a grade of 10.0 for completing the activity and producing all required output, for providing good figures with complete units and captions, and for taking the initiative of implementing the method on 5 different nonlinear CDF's.

References:

[1] 'Enhancement by Histogram Manipulation', 2010 Applied Physics 186 manual by Dr. Maricor Soriano