A5 - Enhancement by Histogram Manipulation

Image is an imitation of the form of an object, place or a person. Appreciation towards images is often proportional to the extent of its quality. However, quality may be affected by many different factors such as lighting, camera resolution, type of focus method, to name a few.

So how do we improve the quality of an image without repeating image acquisition?

--->> The answer is through histogram manipulation.

An image histogram provides us a quick look on the tonal distribution of an image. We can then enhance the quality or certain features of an image by manipulating its pixel value. I'll show you how to do this in this blog post.

First, we obtain from our collection a picture/image that seems to be dark in its nature.

 

Figure 1. Image to be enhanced. 

(image taken from http://baisically.blogspot.com/2011/01/sad-panda-8.html)

We convert the image into grayscale mode and take its histogram. We then obtain the cumulative distribution function(CDF) from the probability distribution function(PDF) or the normalized histogram. In Scilab, this can be done by using the cumulative sum function cumsum(x) where x is a matrix or vector. In simple terms, CDF is the probability that a value will be found less than or equal to an x value.

 Figure 2. Enhancement preliminaries. (a) Grayscale conversion of figure 1.

(b) Grayscale histogram of figure 1. (c) CDF of normalized version of (b).

We do the enhancement by backprojecting the image pixel values to the pixel value of our desired CDF. For example, our desired CDF is a straight increasing line.

Figure 3. Backprojecting method.

We take a grayscale value of x1 and find its CDF value y1. We then trace y1 in the desired CDF as y2. After tracing y1 to y2, we get the corresponding grayscale value x2 of y2. Finally, we replace x1 by x2 in the image concerned. We repeat the process for all grayscale values from 0-255 of our original CDF.

Since we now know the backprojecting method, we create different desired normalized CDF's of linear and nonlinear form.

 

Figure 4. Different desired CDF's. (a) Linear. (b) Quadratic. (c) Cubic.

(d) Gaussian. (e) Logarithmic. (f) Hyperbolic tangent

The CDF's are acquired using the code snippet below:

grayscale = 0:255;

cdf_linear = (1/255)*grayscale;   //linear CDF
cdf_quadratic = ((1/255)*grayscale).^2;   //quadratic CDF
cdf_cubic = ((1/255)*grayscale).^3;    //cubic CDF

a_gauss = 0.01; b_gauss = -((1/255)^2)*log(100);
cdf_gaussian = a_gauss*exp(-b_gauss*grayscale.^2);   //gaussian CDF  Note: cdf value from 0.01 to 1.

a_ln = (exp(1)-1)/255; b_ln = 1;
cdf_ln = log(a_ln*grayscale + b_ln);    //logarithmic CDF 

b_tanh = atanh(-0.99); a_tanh = (1/255)*(atanh(0.99)-b_tanh);
cdf_tanh = (tanh(a_tanh*grayscale + b_tanh))/1.98 + 0.5;     //hyperbolic tangent CDF

To get the corresponding new grayscale values of 0:255 depending on the desired CDF, we invert the equations of our desired CDF's which in turn makes the CDF values of our original image (cdf_original) as our independent variable. You can follow the code snippet below.

grayscale_linear = round(255*cdf_original);
grayscale_quadratic = round(255*sqrt(cdf_original));
grayscale_cubic = round(nthroot((255^3)*cdf_original, 3));
grayscale_gaussian = round(sqrt(-log(cdf_original/a_gauss)/b_gauss));
grayscale_ln = round((exp(cdf_original)-b_ln)/a_ln);
grayscale_tanh = round(1/a_tanh*(atanh(1.98*(cdf_original-0.5))-b_tanh));

After applying the method as described above, the resulting modified images are

 

Figure 5. Modified images based from a CDF of (a) linear, (b) quadratic,

(c) cubic, (d) gaussian, (e) logarithmic and (f) hyperbolic tangent.

To be able to verify whether the modified images have the desired CDF, we take their corresponding normalized histograms(or pdf) and get their CDF.

Figure 6. Histograms based on the CDF type of (a) linear, (b) quadratic,

 (c) cubic, (d) gaussian, (e) logarithmic and (f) hyperbolic tangent.

Figure 7. Retrieved CDF of modified images based on the CDF type of 

(a) linear, (b) quadratic, (c) cubic, (d) gaussian, (e) logarithmic and (f) hyperbolic tangent.

Looking at figures 4 and figures 7, we can say that the CDF's are exactly the same suggesting that the backprojecting method is indeed effective.

Now, we comment on the alteration of the original image according to a particular CDF.

• For a linear CDF, the image became brighter and seems to be equalized.
• For a quadratic CDF, the image is brighter as compared to using a linear CDF.
• For a cubic CDF, the image is even brighter as compared to both the linear and quadratic CDF.
• For a pseudo-gaussian CDF, the image became very bright insinuating image overexposure.
• For a logarithmic CDF, the image is similar to when using a linear CDF with only slight increment in the presence of almost black colors.
• For a hyperbolic tangent CDF, the image became grayish since the histogram shows that more values can be found in the gray region.

The procedure above is coded personally using a programming language, however there are available freewares online that do histogram manipulation. One of the common freeware is GNU Image Manipulation Program (GIMP). A copy of which can be found here. GIMP is a very powerful image processing software comparable to Adobe photoshop.

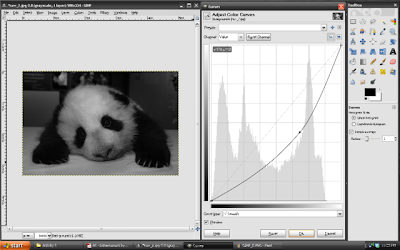
In GIMP, histogram manipulation can be made by first opening your desired image. You can then convert this into grayscale by clicking the Image button and choosing Grayscale in the Mode selection. To automatically graph the histogram of the grayscaled version of your image, click Colors and choose Curves. To start histogram manipulation, just drag the diagonal straight line in the Curves window and observe the changes in the image at the main window. Snapshots of different diagonal line orientations are shown below.

Figure 8. Sample histogram manipulation in GIMP.

 Figure 9. Another sample histogram manipulation using GIMP.

That's it! You can choose whatever CDF you want depending on what effect you would want to happen on your image. Enjoy image enhancement  in the future!

As a conclusion, I would give myself a grade of 10.0 for completing the activity and producing all required output, for providing good figures with complete units and captions, and for taking the initiative of implementing the method on 5 different nonlinear CDF's.

References:

[1] 'Enhancement by Histogram Manipulation', 2010 Applied Physics 186 manual by Dr. Maricor Soriano